How using Euclidean distance vs. Cosine similarity affects KNN results

If you don’t know or forgot how KNN works, please read this great article before moving ahead. Also, if are a bit rusty on the concept of calculating distance between two data points, read this simple article here.

Okay! Hope you’re now comfortable with the basic concepts.

The aim of this article is to -

1. Compare 10 nearest neighbors of a query document when using Euclidean distance vs. Cosine similarity measure to calculate the distance between the two documents
2. Explore why there is a difference in the results

I will use a dataset of wikipedia documents about famous people to build the KNN model and then look at 10 nearest neighbor of Barack Obama. If you want to understand how to process the data to so that it can be fed into the KNN model, read my post on document representation. The dataset that I have used can be found here and the analysis Jupyter notebook here.

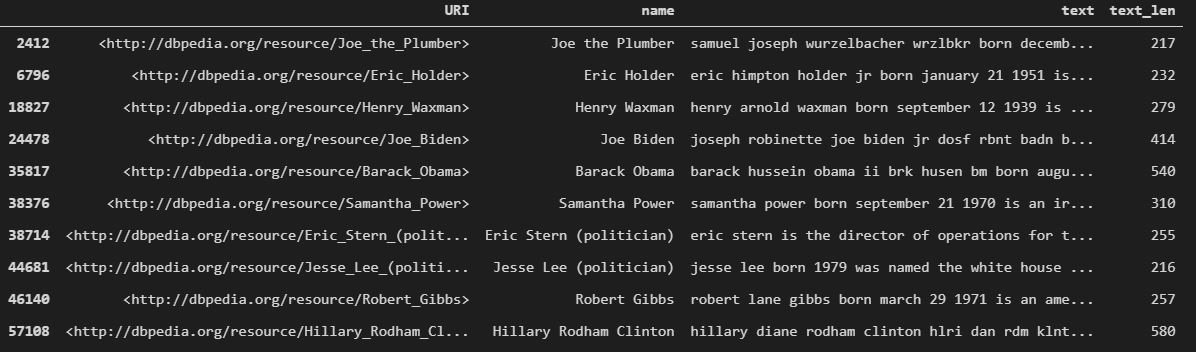
The below picture shows first few rows of the dataset.

First, let’s use the Euclidean distance measure and look at the neighbors. What we can do simply is -

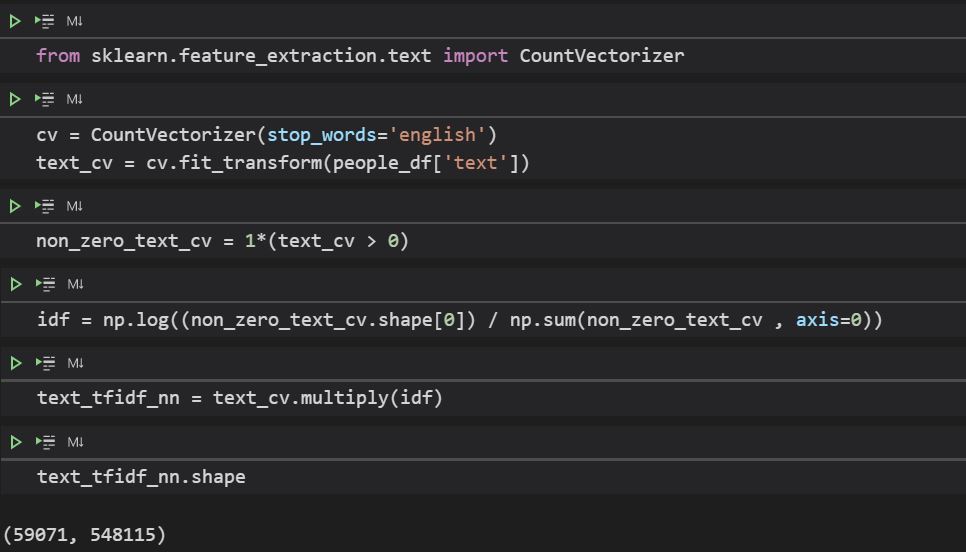
1. Create a bag-of-words representation of the text column of the dataset using sklearn’s CountVectorizer
2. Calculate the IDF of the document using the tfidf formula
3. Multiply the bag-of-words frequencies (TermFrequency) with the IDF values calculated above
4. Build a KNN model with metric parameter as ‘euclidean’
5. Use the model to get top 10 neighbors of Barack Obama

First 3 steps can be done as shown below -

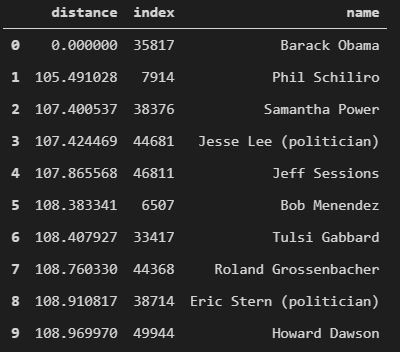
The top 10 results that we get are -

Do you notice something interesting about the results? There can be many things you can come up with, but, one of them is that Joe Biden - who was VP during Obama’s both the terms - is not in the list. Why that might be? We will explore this question further later in the article but for now let’s look at the word length of the articles of these neighbors.

The average word length of Obama’s neighbors’ articles is ~230 words.

Now, let’s compare the results when we use Cosine distance as a metric while building the KNN model. Unfortunately, cosine distance is not directly present as one of the options in sklearn’s implementation of KNN. However, normalizing the input features before passing them into the KNN algorithm has the same effect as using cosine distance. Read this awesome post for more clarity.

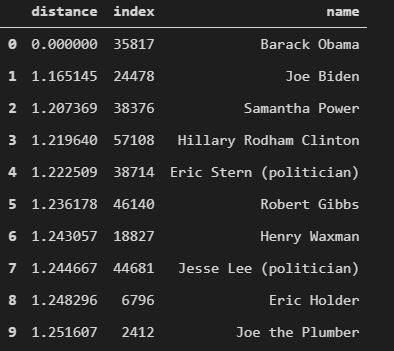
Let’s look at top 10 neighbors when using cosine distance -

Now, we have Joe Biden as the closest neighbor of Barack Obama. And if we see the word lengths of the neighbors’ articles now, we see that the average length is ~306 words (for Euclidean it was ~230 words). Also, Joe Biden’s article is 414 words long.

Explanation

We don’t see Joe Biden in Barack Obama’s top 10 neighbors while using Euclidean distance as the metric because it favors short articles over long articles. Remember that the overall value of euclidean distance depends upon the number of squared terms being added in the square root. Longer the vector, more the distance. On the other hand, Cosine distance removes this bias and let us compare documents of varying lengths.

I did not use TfidfVectorizer to calculate the tfidf representation while calculating the results for Euclidean distance because by default, it normalizes the tfidf vector which we don’t want. Therefore, I first created a bag-of-words model first and then created my own tdidf representation.