Implementing Locality Sensitive Hashing
Scaling document retrieval using Locality Sensitive Hashing
In one of my previous posts, I have covered how we can find similar documents to a query article from a corpus. The problem with the KNN approach is that it is not scalable. For each query article, we have to compute its distance from every other article in the corpus, which - as you can imagine - will be very costly if the corpus becomes large (millions of documents). So what can be done in order to reduce the time taken to find nearest neighbors for a query document?
Let’s take an example - Suppose we have an article for one of the Hollywood actors as a query article. Now, what type of articles should be its closest neighbors? Clearly, the articles should be about the movies the actor was a part of or other co-actors. So, logically, articles about Hollywood movies and actors will be in general “closer” to the query article than let’s say an article about politics or sports. Now, if we can somehow reduce our search space to only these articles, we can reduce the time taken to generate our list of k nearest neighbors. Therefore, we need a way to “group” articles so that we can search for closest neighbors within that group only. This is where we can use something known as Locality Sensitive Hashing or LSH for short.
The basic idea is the divide the training set data points into “bins” and look for nearest neighbors only within bins that are most likely to have nearest neighbors.
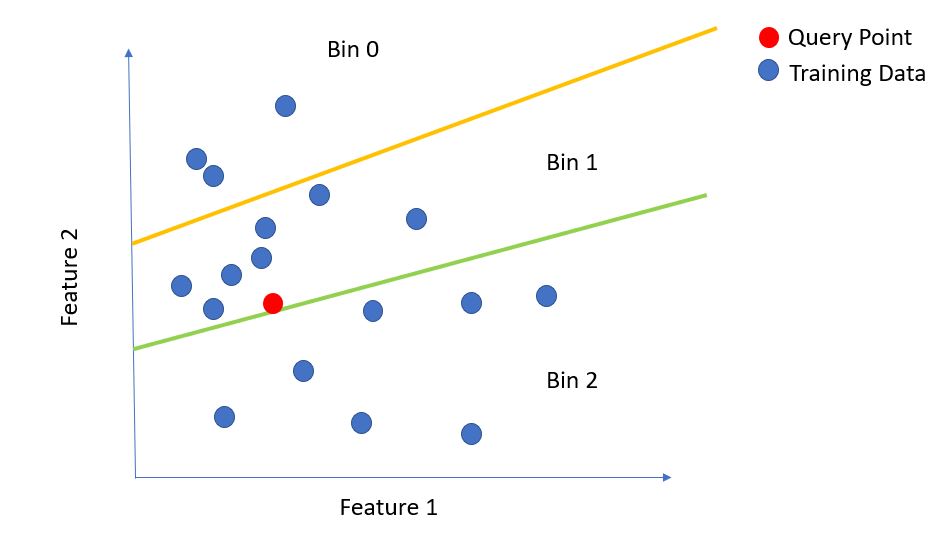
The below figure illustrates the idea -
As we can see, for the red query point, nearest neighbors are most likely to be found in Bin 2. Now, let’s focus on a very big question : how do we come up with these separating lines?
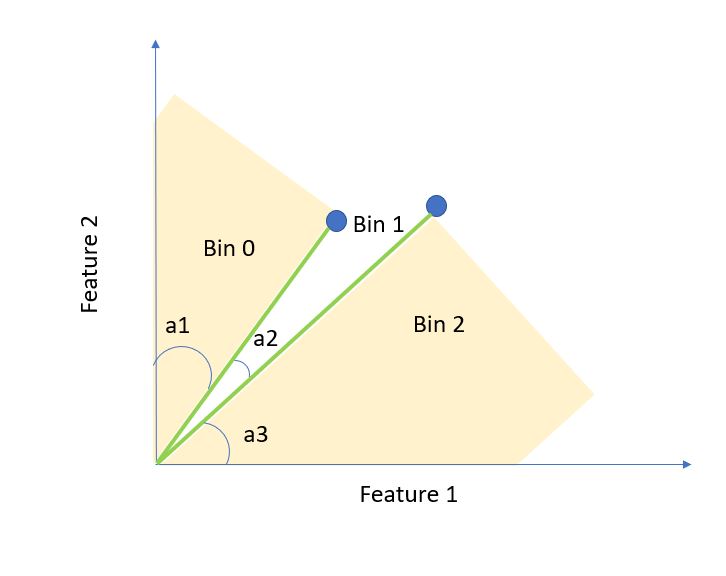
Remember that if two points are closer, the angle between the lines joining the points and the origin will be smaller as illustrated in the figure below -
As you can see, if both the bin separating lines are in region a1 or in region a3 then the points will fall in the same bin and we do not have a problem. However, if one of the lines falls in region a3 then both of the points will fall in different bins and a query point falling in one of the regions will miss the other point. The closer the points lesser the probability the a randomly selected line will fall in between them. So, it does not seem to be a bad idea if we initialize the lines randomly. Finally, in order to solve the problem of nearby points falling in different bins, we can consider “nearby bins” as well while searching for nearest neighbors.